适读人群：正在用 C++/OpenGL 做图形开发、对矩阵变换与 GLM 库的实际用法想“一次啃透”的同学。
目标：搞清楚 GLM 是什么、如何配置；把旋转/平移/缩放/复合变换写对；把变换矩阵顺序、MVP 管线、法线矩阵、动画驱动、常见坑与工程化方案一次讲透。

0. 准备与基本约定

  • 操作系统：Windows / Linux / macOS 均可

  • 编译器：VS / Clang / GCC（C++17 及以上）

  • 渲染：OpenGL 3.3+（示例用到 glUniformMatrix4fv）

  • 数学库：GLM（header-only）

  • 本文统一采用 右手坐标系、列主序矩阵（OpenGL 与 GLM 的天然约定），顶点默认在 NDC 下是 z ∈ [-1, 1]。

1. GLM 是什么？为什么几乎人人都用它

GLM（OpenGL Mathematics） 是一个头文件形式的 C++ 数学库，API 风格贴近 GLSL。它提供：

  • 向量类型：glm::vec2 / vec3 / vec4

  • 矩阵类型：glm::mat2 / mat3 / mat4（列主序，与 OpenGL 保持一致）

  • 四元数：glm::quat

  • 变换工具：glm::translate / rotate / scale / lookAt / perspective / ortho

  • 辅助：glm::radians / degrees / value_ptr 等

优点：
1）贴近着色器思维（GLSL alike），学习成本低；
2）无需编译（header-only），集成简单；
3）跨平台、稳定、成熟。

2. 安装与工程配置（含 CMake / vcpkg / 源码直引）

2.1 vcpkg（Windows & VS 推荐）

vcpkg install glm

CMake 里加上（假设 vcpkg 工具链已配置）：

find_package(glm CONFIG REQUIRED)
target_link_libraries(your_target PRIVATE glm::glm)

2.2 Linux / macOS 包管理

  • Ubuntu / Debian：

    sudo apt-get install libglm-dev

  • macOS（Homebrew）：

    brew install glm

CMake 同上 find_package(glm CONFIG REQUIRED) 即可。

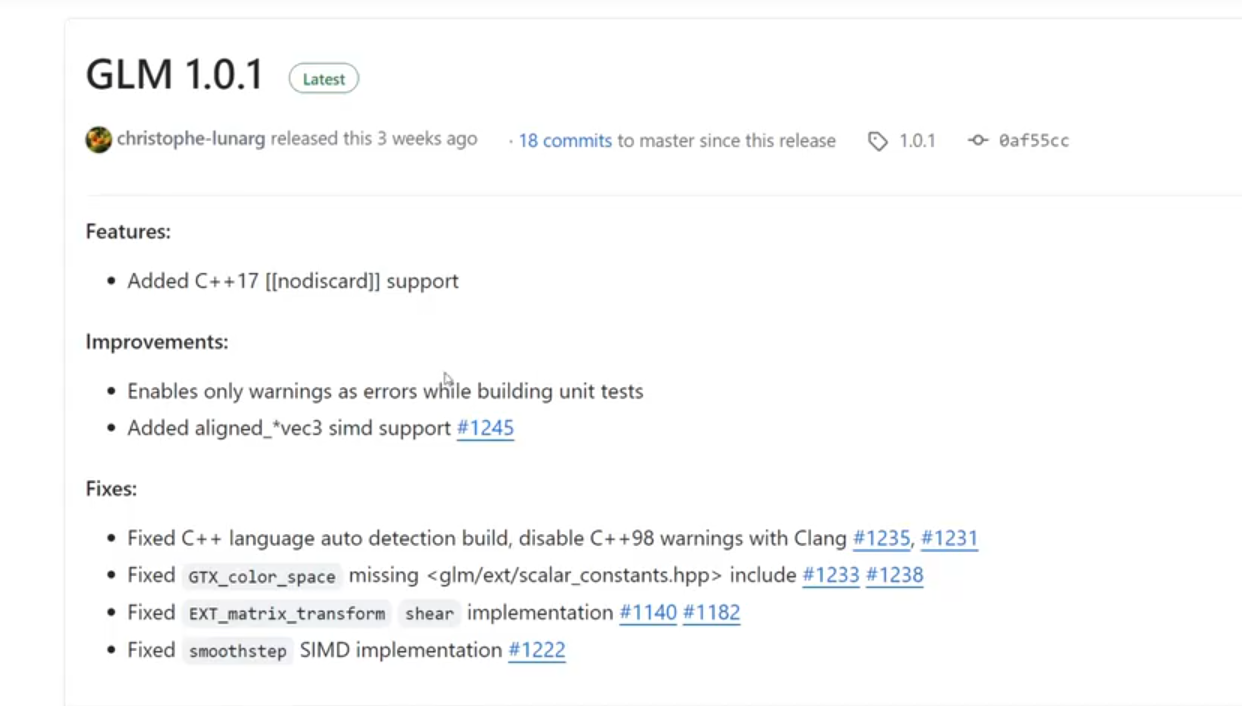
2.3 直接源码（最通用）

  • 从 GitHub 下载 GLM，解压后把 glm/ 放到你的 include/。

  • 代码里直接：

    #include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>

注意：变换函数在 gtc/matrix_transform.hpp，取指针需 gtc/type_ptr.hpp。

3. GLM 的数据结构与内存布局（列主序、很关键）

  • glm::mat4 是 列主序：可以理解为 m[col][row]。

  • OpenGL 传矩阵默认也是列主序，因此 glUniformMatrix4fv(..., GL_FALSE, glm::value_ptr(M)) 无需转置。

  • 若你来自 DirectX/HLSL/行主序思维，请牢记：GLM/GL 默认列主序；不要随便把 transpose 参数设为 GL_TRUE。

4. 角度与弧度，模板类型的“小坑”

GLM 的 rotate 第二个参数是 弧度（radians），不是角度（degree）。
同时，GLM 的函数是 模板函数，经常需要 float 明确类型以免推导歧义。

正确写法：

glm::rotate(glm::mat4(1.0f), glm::radians(90.0f), glm::vec3(0.0f, 0.0f, 1.0f));

易错点：

  • glm::radians(90.0) 少了 f，类型可能推到 double，从而与其它参数不匹配。

  • glm::vec3(0.0, 0.0, 1.0) 也应加 f。

  • 统一用 float 后缀，能避免 90% 的模板推导问题。

5. 变换矩阵原理速通（平移/缩放/旋转）

5.1 平移（Translate）

将点 p 沿 (tx, ty, tz) 平移，可由矩阵：

| 1  0  0  tx |
| 0  1  0  ty |
| 0  0  1  tz |
| 0  0  0  1  |

GLM：

glm::mat4 T = glm::translate(glm::mat4(1.0f), glm::vec3(tx, ty, tz));

5.2 缩放（Scale）

沿各轴缩放 (sx, sy, sz)：

| sx 0  0  0 |
| 0  sy 0  0 |
| 0  0  sz 0 |
| 0  0  0  1 |

GLM：

glm::mat4 S = glm::scale(glm::mat4(1.0f), glm::vec3(sx, sy, sz));

5.3 旋转（Rotate）

绕单位轴 u = (ux, uy, uz) 旋转角 θ（弧度）用罗德里格斯公式，GLM 直接帮你做好：

glm::mat4 R = glm::rotate(glm::mat4(1.0f), theta, glm::vec3(ux, uy, uz));

绕 Z 轴 90°（常见 2D/屏幕空间）：

glm::mat4 Rz = glm::rotate(glm::mat4(1.0f),
                           glm::radians(90.0f),
                           glm::vec3(0.0f, 0.0f, 1.0f));

6. 代码实战：把旋转/平移/缩放写“对”

我们先定义一个全局矩阵 transform 表示“模型矩阵”：

glm::mat4 transform(1.0f);

6.1 旋转

// bug 备忘：rotate 角度必须是弧度，且尽量用 float
transform = glm::rotate(glm::mat4(1.0f),
                        glm::radians(90.0f),
                        glm::vec3(0.0f, 0.0f, 1.0f));

6.2 平移

transform = glm::translate(glm::mat4(1.0f),
                           glm::vec3(0.5f, 0.0f, 0.0f));

6.3 缩放

transform = glm::scale(glm::mat4(1.0f),
                       glm::vec3(0.1f, 0.5f, 1.0f));

6.4 复合：顺序决定一切

glm::mat4 R = glm::rotate(glm::mat4(1.0f),
                          glm::radians(90.0f),
                          glm::vec3(0.0f, 0.0f, 1.0f));
glm::mat4 T = glm::translate(glm::mat4(1.0f),
                             glm::vec3(0.5f, 0.0f, 0.0f));

// 先旋转后平移：等价于 transform = T * R
transform = T * R;

// 先平移后旋转
// transform = R * T;

记忆法：transform * vec 的计算规则是 右边先作用。T * R * v 表示 先 R，再 T。

7. 动画驱动：帧增量 vs. 时间增量（deltaTime）

你的示例：

float angle = 0.0f;
void doRotation() {
    angle += 2.0f;
    transform = glm::rotate(glm::mat4(1.0f),
                            glm::radians(angle),
                            glm::vec3(0.0f, 0.0f, 1.0f));
}

这会产生“与帧率相关”的角速度：高帧率转得更快。更稳妥是用 deltaTime：

float angle = 0.0f; // 单位：度
void doRotation(float deltaTime) {
    const float speed = 45.0f; // 度/秒
    angle += speed * deltaTime;
    transform = glm::rotate(glm::mat4(1.0f),
                            glm::radians(angle),
                            glm::vec3(0.0f, 0.0f, 1.0f));
}

8. 绕任意点旋转：T * R * T⁻¹ 的技巧

若要绕世界中点 C 旋转物体（非原点），套路是：

transform = T(C) * R(θ) * T(-C)

GLM 示例：

glm::vec3 center(1.0f, 2.0f, 0.0f);
glm::mat4 M = glm::translate(glm::mat4(1.0f), center)
            * glm::rotate(glm::mat4(1.0f), glm::radians(30.0f), glm::vec3(0,0,1))
            * glm::translate(glm::mat4(1.0f), -center);

9. 从 Model 到 MVP：与着色器打通

9.1 View（相机）与 Projection（投影）

  • 观察矩阵（View）：用 glm::lookAt(eye, center, up)

  • 投影矩阵（Projection）：透视用 glm::perspective(fovy, aspect, near, far)；正交用 glm::ortho。

示例：

glm::mat4 model(1.0f); // 你的 transform
glm::mat4 view  = glm::lookAt(glm::vec3(0.0f, 0.0f, 3.0f),
                              glm::vec3(0.0f, 0.0f, 0.0f),
                              glm::vec3(0.0f, 1.0f, 0.0f));
glm::mat4 proj  = glm::perspective(glm::radians(60.0f),
                                   width / height,
                                   0.1f, 100.0f);
glm::mat4 mvp = proj * view * model;

9.2 传给着色器

顶点着色器（Vertex Shader）：

#version 330 core
layout(location = 0) in vec3 aPos;
uniform mat4 uMVP;
void main() {
    gl_Position = uMVP * vec4(aPos, 1.0);
}

C++ 侧：

GLuint loc = glGetUniformLocation(program, "uMVP");
glUniformMatrix4fv(loc, 1, GL_FALSE, glm::value_ptr(mvp));
// GL_FALSE：不要转置！GLM/GL 默认列主序

10. 法线矩阵（Normal Matrix）

光照计算需要 法线方向。当模型有非等比缩放时，法线不能用 model * n 简单变换。正确做法：

normalMatrix = mat3( transpose( inverse( model ) ) )

GLM：

glm::mat3 normalMat = glm::transpose(glm::inverse(glm::mat3(model)));

着色器里用 uNormalMatrix * normal 变换。

11. 常见坑与对策清单

1）角度 vs 弧度：glm::rotate 需要弧度，统一用 glm::radians。
2）float 模板：统一写 1.0f / 0.0f / 90.0f 避免 double/float 混淆。
3）矩阵顺序：T * R * S * v 右边先作用。想“先旋转，再平移”，就写 T * R。
4）列主序/转置标志：glUniformMatrix4fv(..., GL_FALSE, ...)，不要乱设 GL_TRUE。
5）右手/左手与深度范围：OpenGL 默认右手与 [-1,1]；若移植到 Vulkan/DirectX，记得检查手性与 Z 范围。
6）视野与近平面：perspective 的 fovy 过小/过大或 near 太近，容易引发 Z-fighting 或畸变。典型设置 near=0.1、far 成倍比 near 大 1000+。
7）动态动画：用 deltaTime 做角速度/位移速度，避免帧率耦合。
8）精度：绝大多数场景 float 足够；超大世界或超远裁剪平面才考虑 double/分层坐标。

12. 工程化与性能：不止能跑，还要跑稳

  • 缓存矩阵：只有参数变化时才重建，不要每帧做无效构造。

  • UBO/SSBO：把公共的 VP、灯光等放入 UBO，每帧只更新一次，多个 Draw 共享。

  • 实例化绘制：相同网格不同变换，用实例化 + per-instance 矩阵（或分解为 TRS）做批量渲染。

  • 避免冗余三角函数：重复旋转的值可以累积角度，用一次 sin/cos，或用四元数累计以减轻漂移。

  • 分解/组合：需要动画插值时，优先对 TRS 或四元数插值，而非对 4×4 直接线性插值。

13. 调试方法：当画面“不对劲”时

  • 打印矩阵：用 glm::to_string（需 #include <glm/gtx/string_cast.hpp>）

    std::cout << glm::to_string(mvp) << std::endl;

  • 哨兵点验证：取一个已知点（如模型局部坐标 (1,0,0)），手算期望位置，与 transform * vec4 的结果对比。

  • 渐进构造：先只用 model，再加 view，最后 projection，定位是哪一级出问题。

  • 检查 glGetError：着色器 uniform 名字拼错、program 未绑定，非常常见。

  • NaN/Inf：非等比缩放后做 inverse 要小心奇异矩阵；必要时加入断言或替代策略。

14. 四元数与插值（避免万向节锁）

  • 欧拉角（pitch/yaw/roll）容易万向节锁；

  • 四元数 用于稳定旋转与插值（slerp），GLM 提供 glm::quat、glm::mat4_cast(quat)。

  • 常见流程：用四元数累计旋转 → 转 mat4 → 与 T/S 组合输出。

15. 速查表（Cheat Sheet）

// 头文件
#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>

// 基本变换
glm::mat4 I = glm::mat4(1.0f);
glm::mat4 T = glm::translate(I, glm::vec3(tx, ty, tz));
glm::mat4 R = glm::rotate(I, glm::radians(deg), glm::vec3(ax, ay, az));
glm::mat4 S = glm::scale(I, glm::vec3(sx, sy, sz));

// 相机与投影
glm::mat4 V = glm::lookAt(eye, center, up);
glm::mat4 P = glm::perspective(glm::radians(fovy), aspect, nearZ, farZ);
glm::mat4 MVP = P * V * (T * R * S);

// 法线矩阵
glm::mat3 N = glm::transpose(glm::inverse(glm::mat3(T * R * S)));

// 传 uniform（列主序，无需转置）
glUniformMatrix4fv(loc, 1, GL_FALSE, glm::value_ptr(MVP));

16. 可运行迷你示例（含 CMake 片段与 Shader）

说明：这里聚焦于 矩阵与 GLM 的最小闭环。窗口/上下文（GLFW/GLAD 或 QOpenGL）初始化不展开，只给核心片段。

CMakeLists.txt（片段）

cmake_minimum_required(VERSION 3.15)
project(glm_transform_demo CXX)
set(CMAKE_CXX_STANDARD 17)

find_package(glm CONFIG REQUIRED) # vcpkg 或系统包
add_executable(demo main.cpp)
target_link_libraries(demo PRIVATE glm::glm)

vertex shader (basic.vert)

#version 330 core
layout(location = 0) in vec3 aPos;
uniform mat4 uMVP;
void main() {
    gl_Position = uMVP * vec4(aPos, 1.0);
}

fragment shader (basic.frag)

#version 330 core
out vec4 FragColor;
void main() {
    FragColor = vec4(1.0);
}

核心 C++（main.cpp 片段：构建矩阵并传给着色器）

#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>
// ... 省略：加载GL函数、编译链接着色器、创建VAO/VBO ...

float timeSeconds = /* 你自己的计时获取 */;
float angleDeg    = 45.0f * timeSeconds; // 45度/秒

glm::mat4 model = glm::mat4(1.0f);
model = glm::translate(model, glm::vec3(0.5f, 0.0f, 0.0f));
model = glm::rotate(model, glm::radians(angleDeg), glm::vec3(0.0f, 0.0f, 1.0f));
model = glm::scale(model, glm::vec3(0.5f, 0.5f, 1.0f));

glm::mat4 view = glm::lookAt(glm::vec3(0.0f, 0.0f, 3.0f),
                             glm::vec3(0.0f, 0.0f, 0.0f),
                             glm::vec3(0.0f, 1.0f, 0.0f));

float aspect = static_cast<float>(windowWidth) / windowHeight;
glm::mat4 proj = glm::perspective(glm::radians(60.0f), aspect, 0.1f, 100.0f);

glm::mat4 mvp = proj * view * model;

glUseProgram(program);
GLint loc = glGetUniformLocation(program, "uMVP");
glUniformMatrix4fv(loc, 1, GL_FALSE, glm::value_ptr(mvp));
// ... 绑定VAO，glDrawArrays 或 glDrawElements ...

17. 与你的示例对照：逐段校验要点

你文中的小函数非常标准。强烈建议做以下“加固”：

  • 旋转函数：确保 glm::radians(angle) 的 angle 是 float（float angle = 0.0f;）。

  • 帧驱动 → 时间驱动：将 angle += 2.0f; 替换为 angle += speed * deltaTime;。

  • 复合顺序：想“先旋转后平移”，就写 transform = T * R;；相反则 R * T。

  • 类型一致：glm::vec3(0.0f, 0.0f, 1.0f) 一律加 f 后缀。

  • 用 glm::mat4(1.0f) 作为每次变换的基底，避免历史残留误叠加（除非你就是想累计）。

18. 进阶话题指路

  • 分解与重组：把 mat4 分解为 T/R/S（例如 UI 编辑器、动画系统），GLM 有 glm::decompose（需 gtx/matrix_decompose.hpp）。

  • 屏幕对齐（billboard）：构造使对象朝向相机的旋转矩阵。

  • 约束旋转（限制俯仰/偏航）：对欧拉角加 clamp，或对四元数施加约束。

  • 坐标空间条理：Object → World → View → Clip → NDC → Screen，每一步都可打印检查。

19. QA：常见疑问速答

Q：为什么我传 glUniformMatrix4fv 要用 GL_FALSE？
A：GL/GLM 用列主序存放，函数参数 transpose 传 GL_FALSE 即可。除非你用行主序矩阵，才需要转置。

Q：为什么模型“绕原点转”，而不是“原地自转”？
A：你的模型局部原点不在几何中心；或你先平移再旋转了。绕任意点旋转要用 T(C) * R * T(-C)。

Q：法线变了方向，光照乱了？
A：有非等比缩放时，法线必须用 normalMatrix = transpose(inverse(mat3(model))) 来变换。

Q：near/far 该怎么取？
A：near 越大、far/near 比例越小，Z 精度越好。经验：near=0.1 或 0.2、far=100~1000，按场景调整。

20. 小结

  • GLM 的配置极其简单，但用“对”很重要：弧度、float、列主序、变换顺序 是四大关键。

  • 现场代码（旋转/平移/缩放/复合）+ MVP/法线矩阵/动画驱动，是日常渲染的最小闭环。

  • 工程化阶段请上 UBO/实例化/缓存策略，调试时用打印与哨兵点逐级定位。

  • 进一步可把 Euler 转换为四元数，解决万向节锁与平滑插值问题。

如果你愿意，我可以把这篇文章再整合成单文件 Demo（含最小 GLFW/GLAD 初始化、可编译运行），以及一版专讲“绕任意点旋转 + 自转公转”的交互示例，方便你直接展示与教学。

# 策略模式 # 图形渲染 # c++
Logo
CSDN-OPC开发者社区

这里是“一人公司”的成长家园。我们提供从产品曝光、技术变现到法律财税的全栈内容，并连接云服务、办公空间等稀缺资源，助你专注创造，无忧运营。

更多推荐

cover

『低代码开发的终极形态：AI 驱动的可视化编程』

avatar CSDN-OPC开发者社区
cover

上下文工程完全指南：打造高确定性AI Agent的四大支柱（建议收藏）

avatar CSDN-OPC开发者社区

Python内存管理终极指南：优化大型数据集处理性能的5个技巧

Python内存管理在处理大型数据集时常常成为性能瓶颈，掌握有效的内存优化技巧能让你的程序运行速度提升数倍。在python-mastery课程中，我们深入探讨了如何通过不同的数据结构选择来显著降低内存使用。## 🚀 为什么Python内存管理如此重要？当处理像芝加哥公交系统数据（包含577,000多行记录）这样的大型数据集时，内存使用可能从12MB激增到50MB以上！这不仅仅是数字问题，

avatar CSDN-OPC开发者社区